步骤:识别频率响应
成功识别后,受控系统的频率响应显示在波德图中:
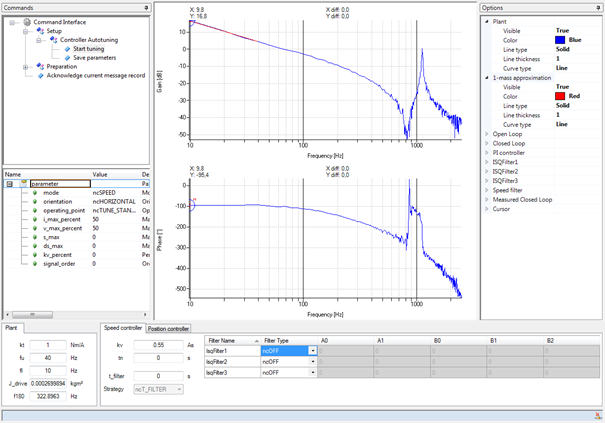
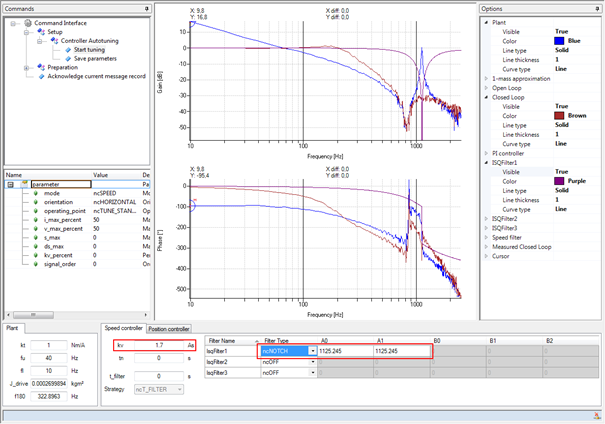
图: 频率响应的识别
对频率响应的识别:
•粘性摩擦很低,由于10-40Hz范围内的-20 dB/decade的直线
•共振频率(fres)为1125Hz
•反共振频率(fares)为812Hz
•相位交越频率(f180)为323Hz
•质量惯性矩的估计值为0.00027 kgm²。
步骤:对标准配置的评估
SLO计算出一个增益,导致以下特点:
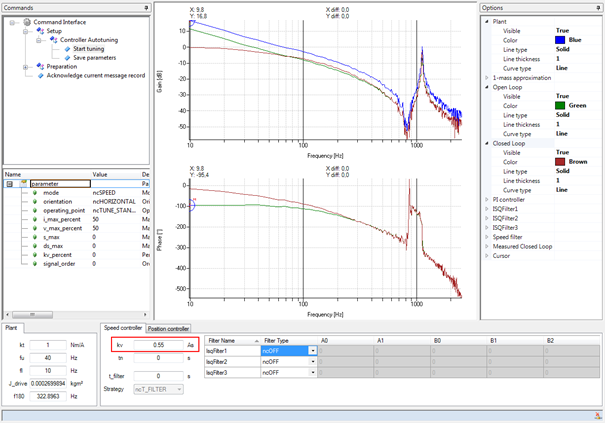
图:对标准配置的评估
闭合环路的波德图显示,图中闭合环路的设计规范所要求的特性并没有得到满足。 在低频时,振幅响应既不在0dB,在高频时,振幅响应也没有以足够的陡度下降。共振大大高于相位交越频率,是对增益的限制。
由于这个原因,我们将尝试用滤波器来改善这些特性。
步骤:使用不同的滤波器进行整定
用低通滤波器整定
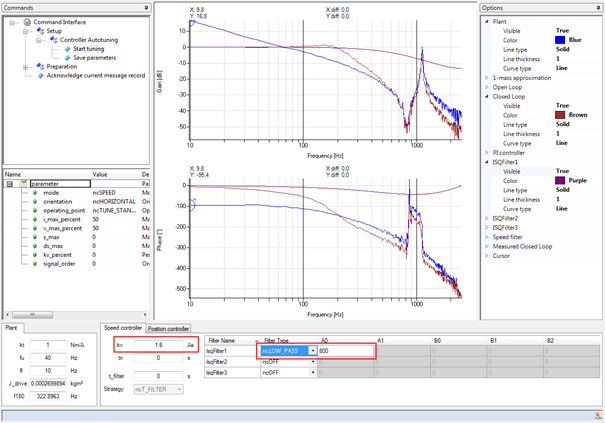
图: 用低通滤波器整定
闭合环路的波德图显示,图中闭合环路的设计规范所期望的特性并没有完全得到满足。低频的振幅响应在0dB线上,但共振几乎达到了0dB线。因此,高频率下的振幅响应并没有以足够的陡度下降。
用双二阶滤波器整定
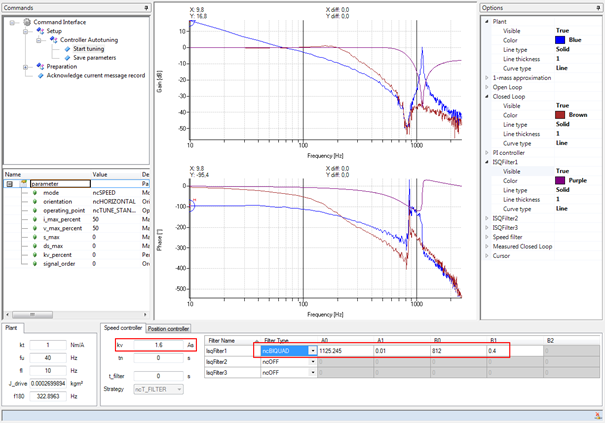
图:用双二阶滤波器整定
闭合环路的波德图显示, 完全满足了图中闭合环路设计规范的预期特性。
用notch滤波器整定
闭合环路的波德图显示, 完全达到了图中闭合环路的设计规范所要求的特性。甚至有可能实现比双二阶滤波器更高的增益。
结论
在这个双质量的系统中使用一个notch滤波器或双二阶滤波器可以实现对设定点变化的可用响应。由于可实现的增益较高,notch滤波器更受欢迎。