步骤:识别频率响应
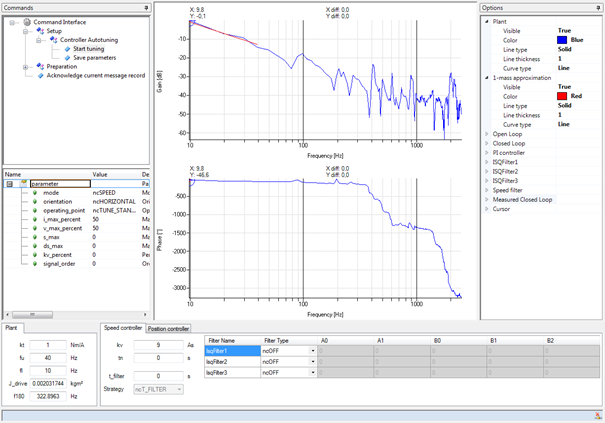
成功识别后,受控系统的频率响应显示在波德图中:
图: 频率响应的识别
对频率响应的解释:
•粘性摩擦很低,由于10-40Hz范围内的-20 dB/decade的直线
•由共振和反共振组成的多个有序配对
•最低共振频率(fres)为100Hz
•最低反共振频率(fares)为80Hz
•相位交越频率(f180)为323Hz
•在相位交越频率(有问题的)之上的额外共振频率(411Hz、606Hz、900Hz、2015Hz)。
•质量惯性矩的估计值为0.002 kgm²。
步骤:对标准配置的评估
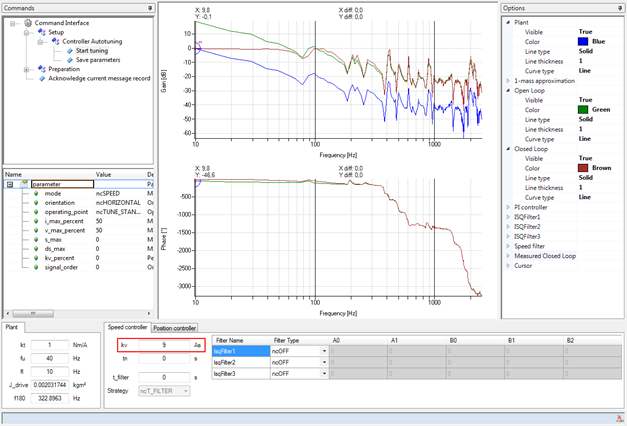
SLO计算出一个增益,导致以下特点:
图: 对标准配置的评估
闭合环路的波德图显示,图中闭合环路的设计规范所期望的特性并没有完全得到满足。尽管对频率为60Hz的设定值变化的响应是足够的,但在更高频率下的振幅响应并没有足够陡峭的下降(共振部分一直延伸到0dB线)。
由于这个原因,我们将尝试用滤波器来改善其特性。最低的共振频率低于相位交越频率(fres < f180),但在相位交越频率以上仍有额外的共振问题。由于这个原因,使用低通滤波器或双二阶滤波器可以改善特性。由于共振的数量,使用几个notch滤波器是没有意义的。
步骤:使用不同的滤波器进行整定
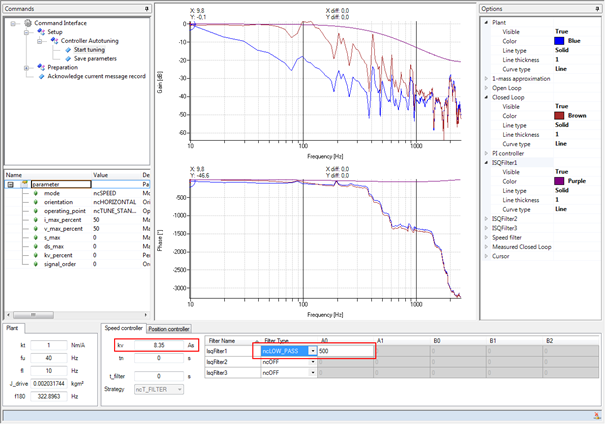
用低通滤波器整定
图: 用低通滤波器整定
低通滤波器的使用大大降低了闭环在高频率下的振幅响应。尽管使用了这个滤波器,还是可以实现相当的增益。
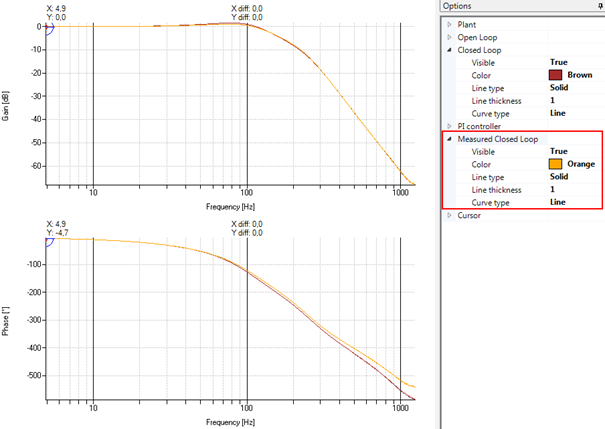
用双二阶滤波器整定
图: 用双二阶滤波器进行整定
使用双二阶滤波器大大改善了闭环在高频率下的振幅响应。然而,可实现的增益要比使用低通滤波器的少。
结论
对这种多质量系统使用低通滤波器可以实现对设定值变化的可用响应。