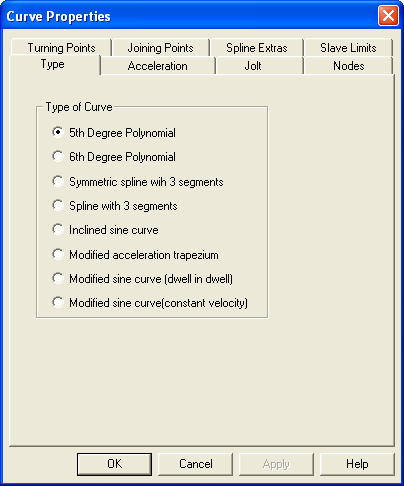
插值的类型决定了所使用的计算。
该编辑器支持以下类型的计算:
1. 多项式函数
2. 多项式样条曲线
3. 使用多项式样条曲线对正弦曲线进行逼近
在下文中,插值曲线的端点被标示为 P0=(x0,y0) and P1=(x1, y1)两个坐标点。这两点之间的插值曲线要确定的函数被标为f。 曲线左端点的一阶导数是 dy0,右端点一阶导数是dy1。同样的,左端点的二阶导数是ddy0,右端点二阶导数是ddy1。
多项式函数和多项式样条曲线可以用于所有的运动转换,正弦曲线只能用于某些运动(静止到静止或恒速到恒速)。由于其端点的属性导致而不能用于该插值的曲线类型,不能被选择(呈灰色)。
五阶多项式函数
一个五阶多项式函数, f(x) = a0+a1x+a2x2+a3x3+a4x4+a5x5,有六个系数。 它们是通过两个端点输入的函数值、一阶和二阶导数值来确定的。
•f(x0) = y0
•f(x1) = y1
•f´(x0) = dy0
•f´(x1) = dy1
•f´´(x0) = ddy0
•f´´(x1) = ddy1
由于凸轮函数及其一阶导数应该是常数,所以五阶多项式函数唯一可以选择的是 曲线两端的二阶导数的值。五阶多项式函数是默认的插值曲线的类型。
六阶多项式函数
一个六阶多项式函数的七个系数, f(x) = a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6, 并非完全通过输入函数值、两个端点的一阶和二阶导数来确定。
对于剩下的(第七个)条件,你可以:
1.在P0 和 P1之间指定一个 插值点P2=(x2,y2),曲线应通过该点,即f(x2)=y2
2.指定曲线 转折点 (x2)的第一个坐标: x0 < x2 < x1,这样 f''(x2) = 0
3.指定左端点的 三阶导数 的值:f'''(x0) = dddy0
4.指定右端点的 三阶导数 的值:f'''(x1) = dddy1
如果用户没有设置以上4个条件之一,则只会计算出五阶多项式函数(即a6 = 0)。
三段式通用样条曲线
如果一个函数由多个分段式的多项式函数组成,则该函数被认为是一个多项式样条曲线:
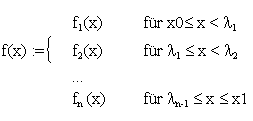
其中fi(x)是多项式函数。
对于一个由3个六阶多项式函数组成的多项式样条曲线,21个系数和3个多项式之间的2个连接点(l1 and l2)都必须被确定。这23个条件中的6个是由端点的函数值和一、二阶导数的值决定的,另外8个是由函数为常数的要求和连接点l1 和 l2的前三个偏差值决定的。
最后,这些连接点的位置是计算所需的。l1 和 l2的值 可以 由用户选择。默认情况下,连接点被放置在x0 和 x1之间距离的1/3和2/3处。这就留下了7个自由度。为了将自由度降低到一个合理的水平,选择仅限于以直线为中间多项式样条曲线。这可能也是最常见的样条曲线类型,因为它很容易实现两个端点之间的平滑运动。
这就只留下两个可用的条件供用户选择:
1.指定 左端点的三阶导数的值 :f1'''(x1) = dddy0
2.指定 右端点的三阶导数的值 :f3'''(x2) = dddy1
3.指定 第一个连接点的函数值:f(l1)=fl1
4.指定 第二个连接点的函数值:f(l2)=fl2
5.连接点的四阶导数的一致性(2个条件):f1''''(l1) = f2''''l1), f2''''(l2) = f3''''(l2)
6.指定 P0 和 P1之间的插值点 (x2,y2),曲线应该通过这些插值点:f(x2)=y2
7.指定 曲线的转折点x2 :f''(x2) = 0
8.选择 直线的斜率
如果用户选择的条件少于两个,则按以下顺序增加附加条件:
1.左端点的三阶导数设置为0。
2.右端点的三阶导数设置为0。
这两个条件使插值曲线在两端的三阶导数。
三段式对称样条曲线
这是一种特殊的 具有3个多项式函数的多项式样条曲线,当端点的一阶导数相同(f´(x0)=f´(x1)),端点的二阶导数相反(f''(x0)=-f''(x1)) 时可以使用。在这种情况下,有3个自由度,而不是一般多项式样条曲线的7个自由度。
这些可以从以下条件中选择:
1.选择第一个 连接点;这将导致第二个连接点的位置的对称性
2.指定 左端点的三阶导数的值 :f1''(x0) = dddy0;这也确定了右端点的三阶导数的值
3.指定 第一个连接点的函数值:f(l1)=fl1;这也确定了第二个连接点的函数值
4.连接点的四阶导数的一致性:f1''''(l1) = f2''''(l1)
5.对称点的的鞍点:f2'''((x0+x1)/2) = 0;这使对称点处的速度曲线变平了
6.在P0 和 P1之间指定 额外的点 (x2,y2),曲线应该通过这些点:f(x2)=y2
7.指定 曲线的转折点x2 f''(x2) = 0
8.为中间的多项式函数选择一条线 ( = 2条件)
9.选择 直线的斜率
条件5和8不能同时选择。如果是直线,转折点不能在中间段。
如果用户选择的条件少于三个,凸轮编辑器会添加额外的条件:
如果仍然有三个条件空缺,则使用一条直线作为第二段,并将端点的三阶导数设置为0(恒定三阶导数)。
如果仍然有两个条件空缺 ,并且如果已经为三阶导数输入了一个值或者选择了一个恒定的四阶导数,那么将使用一条直线作为第二段。否则,端点的三阶导数被设置为0,连接点的四阶导数被选择为常数。
如果只有一个条件空缺 ,并且第二段被设置为直线,那么端点的三阶导数被设置为0。如果选择了一个鞍点和恒定的三阶导数,那么最终的条件是恒定的四阶导数。
如果选择了一个鞍点 ,但不是一个恒定的三阶导数,则在端点设置一个恒定的三阶导数。最后,如果前两个条件中没有设置鞍点,则在最后一个可用条件中设置。
倾斜正弦曲线 静止到静止
对于静止到静止的运动 (dy0=0, dy1=0, ddy0 = 0, ddy1 = 0), 倾斜的正弦曲线 (VDI 指南2143 "凸轮机构的运动规则;理论基础",1980年10月,第6.1节) 可用于内插曲线。 曲线的转折点的位置 可以由用户指定。
根据VDI的说法,倾斜的正弦线产生的抖动特别小(三阶导数)。沿着这条曲线的运动具有较低的震荡,因此适合于高速运动。另一方面,速度、加速度和动态扭矩的最大值比 五阶多项式要高。
倾斜的正弦线可以用多项式样条曲线来近似。对于一个标准化的倾斜正弦曲线,计算表明,一个有6段的多项式样条曲线能以6*10-8的精度接近倾斜正弦线,一阶导数的精度为2*10-6 ,二阶导数的精度为8*10-5。
修正的加速度梯度曲线 静止到静止
对于静止到静止的运动(dy0=0, dy1=0, ddy0 = 0, ddy1 = 0), 修正的加速度梯度曲线(VDI 指南2143,第6.1节)可用于内插曲线。与倾斜的正弦线一样, 可以输入曲线转折点的位置。
对于一个标准化的修改后的加速度梯度曲线,计算表明,一个有6段的多项式样条曲线可以近似修改后的加速度梯度曲线,其精度为2*10-7。一阶导数的误差小于2*10-5;二阶导数的误差小于9*10-4。
修正正弦曲线 静止到静止
对于静止到静止的运动 (dy0=0, dy1=0, ddy0 = 0, ddy1 = 0), 修改的正弦线(VDI 指南2143,第6.1节)可用于内插曲线,并可输入曲线转折点的位置 。
VDI 2143报告说,修改后的正弦线的优点是速度、加速度和动态扭矩的最大值较低,因此适合于高速行驶。然而,最大震荡值比倾斜的正弦线或 五阶多项式要高 。
对于一个标准化的修正正弦线,计算表明,一个有6段的多项式样条曲线可以以2*10-6的精度接近修正正弦曲线。一阶导数的误差小于5*10-5;二阶导数的误差小于1*10-3。
修正正弦曲线 恒定速度到恒定速度
修正正弦曲线也可用于从恒定速度到恒定速度的运动(ddy0 = 0, ddy1 = 0)。用户可以指定 转折点 的位置 (0 < l < 1)。
根据 VDI 指南2143,对于需要在运动部分有转折点的运动,应该使用修正正弦曲线而不是 五度多项式函数,因为多项式函数在各种情况下都会过冲。通过用4段的多项式样条曲线近似,这个修正正弦曲线可以以10-5的精度接近 (一阶导数的误差大约为10-4;二阶导数的误差大约为10-3)。